Probability Evaluation Study of Soil Erosion Types in the Songhua River Basin Based on Deep Learning and Gaussian Kernel Density Estimation
-
摘要:
目的 为科学判别流域尺度土壤侵蚀类型并给出相应的发生概率。 方法 构建基于深度学习(deeplearning, DL)的松花江流域土壤侵蚀模数(erosion modulu, EM)计算模型, 并计算不同类型的侵蚀模数。以降雨、气温、风速3个侵蚀模数影响因子为随机变量, 利用数值模拟和高斯核密度估计法(gaussian kernel densityestimation, GKDE)构建EM概率评价方法, 给出不同土壤侵蚀强度组合的发生概率。 结果 EM计算模型验证期的R2均>0.86。流域内平均每年有74.47%发生微度水蚀与微度风蚀; 12.86%的面积发生轻度及以上水蚀与微度风蚀; 12.56%的面积发生轻度及以上风蚀与微度水蚀; 0.11%的面积水蚀强度与风蚀强度均在轻度及以上。36个典型像元中, 发生微度水蚀与微度风蚀的平均概率为57.45%;发生微度水蚀与轻度风蚀的平均概率为30.26%;发生微度水蚀与中度风蚀的平均概率为8.03%;发生轻度水蚀与微度风蚀的平均概率为2.11%;发生微度水蚀与重度风蚀的平均概率为2.08%;发生其余强度组合的平均概率在0.05%以下。 结论 构建的松花江流域EM计算模型精度较高, 揭示了松花江流域土壤侵蚀类型空间分布特征, 并给出不同土壤侵蚀强度组合的发生概率, 为松花江流域土壤侵蚀治理提供依据。 Abstract:Objective To scientifically identify the types of soil erosion at the watershed scale and give the corresponding probability of occurrence. Methods This study constructs a deep learning (DL)-based model for calculating soil erosion modulus in the Songhua River Basin and calculates different types of soil erosion modulus. Using three erosion modulus influencing factors, namely rainfall, air temperature and wind speed, as random variables, numerical simulation and Gaussian Kernel Density Estimation (GKDE) were used to construct the EM probability evaluation method, which gives the probability of occurrence of different combinations of soil erosion intensities. Results The R2 of the validation period of the EM computational models were all >0.86; 74.47% of the average annual occurrence of slight water erosion and slight wind erosion in the watershed; 12.86% of the area of slight and above water erosion and slight wind erosion; 12.56% of the area of slight and above wind erosion and slight water erosion; 0.11% of the area of water erosion strength and wind erosion intensity are both slight and above. 36 typical image elements of the 36 typical images, the average probability of occurrence of slight water erosion and slight wind erosion is 57.45%; the average probability of occurrence of slight water erosion and mild wind erosion is 30.26%; the average probability of occurrence of slight water erosion and moderate wind erosion is 8.03%; the average probability of occurrence of mild water erosion and slight wind erosion is 2.11%; the average probability of occurrence of slight water erosion and severe wind erosion is 2.08%; and the evaluations of occurrence of the remaining combinations of probabilities were all below 0.05%. Conclusion The calculation model of erosion modulus in the Songhua River basin constructed in this study has high accuracy, reveals the spatial distribution characteristics of soil erosion types in the Songhua River basin, and gives the probability of occurrence of different combinations of the intensity of the two types of erosion, which provides a basis for the management of soil erosion in the Songhua River basin. -
松花江流域位于中国东北地区，该流域拥有珍贵的黑土资源，也是我国重要的粮食产区和商品粮基地。由于人类活动和自然因素的影响导致该流域土壤侵蚀问题尤为严重，自20世纪50年代以来, 流域内黑土平均厚度减少约40 cm[1]。因此, 有必要对该流域土壤侵蚀规律进行深入研究。
松花江流域内存在水蚀、风蚀2种不同的土壤侵蚀类型[2]，WANG等[3]使用同位素示踪法研究该流域水蚀、风蚀的成因；左小锋等[4]通过风洞试验研究黑土区前期风蚀与水蚀相互作用；WANG等[5]通过经验方程对东北地区近20年不同土壤侵蚀类型进行量化分析松花江流域内风蚀、水蚀的变化趋势；吴瀚逸等[6]、杨严攀等[7]、池金洺等[8]分别基于不同分辨率的地形、气象、土地利用等数据产品通过经验方程计算包括松花江流域在内不同研究区域的土壤侵蚀模数，发现其所表征的对应研究区域内土壤侵蚀空间分布特征均具有较好的代表性；国外学者[9-10]基于深度学习(DL)构建区域水蚀或风蚀及其影响因子的预测模型，并分析侵蚀影响因子与侵蚀之间的映射关系。
当前基于经验方程的侵蚀模型和基于DL构建的侵蚀模型的研究多单独针对水力侵蚀或风力侵蚀及其相应影响因子开展研究。但部分因子对2种侵蚀都有贡献[11]，目前与此相关的研究较少。土壤侵蚀的部分影响因子(如降雨、风速、气温等)具有较强的随机性[12]，使得土壤侵蚀的评价结果也具有随机性，即某土壤侵蚀评价结果应具有其相应的发生概率。因此，开展土壤侵蚀类型的概率评价研究能够更好地考虑其影响因素的随机性，给出具有更丰富决策参考信息的概率评价结果[13]。
土壤侵蚀可能是由水蚀、风蚀共同作用导致的，科学识别土壤侵蚀类型及其在空间的分布，并给出其发生概率是值得研究的一个课题。为更好地揭示松花江流域土壤侵蚀类型及其空间分布，本研究结合土壤侵蚀的经验方程的土壤侵蚀量化结果，构建基于DL的侵蚀模数(erosion modulu，EM)计算模型，使其可以区分土壤侵蚀类型的同时计算相应类型的土壤侵蚀模数；采用非参数拟合技术获取土壤侵蚀随机影响因子的概率密度，进而利用数值模拟方法创建土壤侵蚀模数随机影响因子样本，并采用高斯核密度估计法构建基于水蚀风蚀联合概率分布的土壤侵蚀概率评价方法，概率评价结果可为区域土壤侵蚀治理提供科学的决策依据。
1. 材料与方法
1.1 研究区概况
松花江是黑龙江的最大支流，全长约2 309 km，流域面积55.68万km2，位于中国东北部(119°52′—132°31′E，41°42′—51°38′N)，主要涵盖黑龙江省与吉林省的大部及内蒙古部分区域(图 1)。流域内的地形以平原为主，其中包括位于中部的松嫩平原和东北部的三江平原，海拔为50~200 m；流域的西部为大兴安岭，东部为长白山，普遍海拔为700~2 700 m。松花江流域属于北温带季风气候，夏季温热多雨，冬季寒冷干燥。年内温差较大，多年平均降水量为500 mm，平均气温3~5 ℃，平均风速2~3 m/s。
图 1 松花江流域位置Fig. 1 Map of the Songhua River basin location
下载:
全尺寸图片
1.2 数据准备
研究数据以松花江流域现有的土壤侵蚀空间数据及地形、地质、气候、土地利用等数据来训练DL模型。
1.2.1 EM影响因子数据
根据已有关于土壤侵蚀因素的相关研究[9, 14-15]，结合松花江流域黑土区土壤侵蚀机理的研究成果[16]，同时考虑数据的可获取性，初步选定14个可能影响松花江流域水力侵蚀模数(water erosion modulus, EMwa)、风力侵蚀模数(wind erosion modulus, EMwi)的驱动因子，将其按属性划分为4类：地形因素(海拔、坡度、坡向、坡长、水流强度指数、地形湿度指数)、气候因素(气温、降雨、风速、积雪)、土地利用因素(植被覆盖度NDVI、土地利用LC)及土壤因素(黏粒、砂粒、粉粒及土壤有机碳含量SOC)。
(1) 地形因素
海拔、坡度、坡向、坡长、水流强度指数(stream power index，SPI)、地形湿度指数(topographic wetness index，TWI)均可在数字高程数据(DEM)中提取、计算得到[15]。本研究使用的数字高程数据(DEM)来源于 http://earthexplorer.usgs.gov网站，网站提供的DEM数据有30 m×30 m与90 m×90 m分辨率精度。本研究选用的DEM数据分辨率为30 m×30 m。
(2) 气候因素
本研究的气象数据来源为中国地面气候资料日值数据集(V3.0)。整理松花江流域内36个气象站点的年降雨量、年平均风速、年平均日最高气温3项气象数据资料，气象站点位置见图 1，本研究所需的时间序列为2001—2020年，使用“克里金法”将数据插值为100 m×100 m分辨率的栅格数据。
由于受到高纬度的影响，应考虑积雪覆盖时长对土壤侵蚀的影响[17-18]。积雪覆盖时长数据来源于国家冰川冻土沙漠科学数据中心(http://www.ncdc.ac.cn)的MODIS中国积雪物候数据集[19-20]，本研究所需的时间序列为2001—2020年，分辨率为500 m×500 m。
(3) 土地覆盖因素
本研究使用的土地利用类型数据为中国土地覆盖数据集(CLCD)[21]，该数据的分辨率为30 m×30 m，按照土地利用类型分类规则将该数据分为耕地、林地、草地、水域、建设用地及荒地。本研究使用的NDVI数据为中国月度植被指数(NDVI)空间分布数据集，分辨率为1 km×1 km。数据来源于资源环境科学数据注册与出版系统(https://www.resdc.cn/data.aspx?DATAID=254)。采用最大值镶嵌法将月尺度NDVI数据处理为年尺度。本研究所需要的土地利用类型及NDVI数据时间序列均为2001—2020年。
(4) 土壤因素
本研究土壤数据来源于国家青藏高原科学数据中心(https://doi.org/10.11666/00073.ver1.db)的中国高分辨率国家土壤信息网格基本属性数据集(2010—2018)[22]。该数据有250 m×250 m和1 km×1 km 2种分辨率，每类数据分为7种不同的深度。本研究使用的黏粒、粉粒及砂粒数据为0—20 cm深度、SOC为5—15 cm深度，分辨率均250 m×250 m[23]。将搜集到的16个影响因子栅格数据重采样为100 m×100 m分辨率。
1.2.2 土壤侵蚀模数空间分布数据
(1) 水力侵蚀模数
本研究使用的土壤水蚀数据为吴瀚逸等[6]制作的2001—2020年中国东北区域土壤水蚀数据集，该数据集分辨率为250 m×250 m。该数据集基于RUSLE模型，对模型每个因子选取多种经典算法进行排列组合计算，结合水文站实测数据直接验证筛选最优算法组合，得到东北地区水力侵蚀模数估算结果。该数据具有较高的时空分辨率和实际精度，可为东北区域的土壤侵蚀评估及水土保持决策提供基础数据。
(2) 风力侵蚀模数
土壤风蚀数据由已被证明在中国东北地区具有较好适用性的通用风蚀方程(RWEQ)计算得到[5]，该方程具体计算方法为：
$$ S L=\frac{2 z}{S^2} Q_{\max } \mathrm{e}^{-\left\{\frac{z}{s}\right\} 2} $$ (1) $$ Q_{\max }=109.80\left(W F \times E F \times \mathrm{SCF} \times K^{\prime} \times C\right) $$ (2) $$ S=150.71\left(W F \times E F \times \mathrm{SCF} \times K^{\prime} \times C\right)^{-0.371\;1} $$ (3) 式中：SL为实际风蚀量(kg/m2)；Qmax为风力最大输沙能力(kg/m)；S为关键地块长度(m)；z为下风向距离(m)，本次计算取50 m[24]；WF为气候因子(kg/m)；EF为土壤可蚀性百分比(%)；SCF为土壤结皮因子；K′为土壤糙度因子；C为植被因子。上述因子计算方法及部分参数的选取参考现有研究[24]。基于RWEQ计算2001—2020年松花江流域风力侵蚀模数。
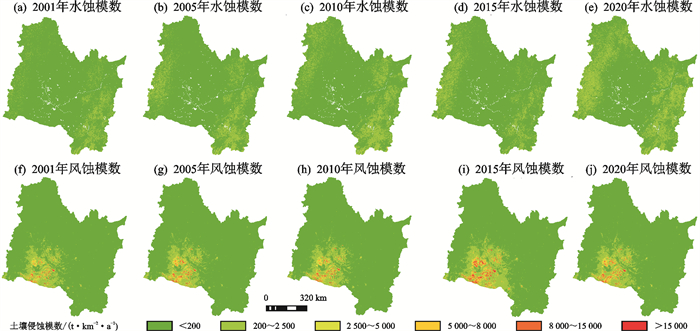
将风蚀模数、水蚀模数分辨率重采样为100 m×100 m，基于重采样后的数据绘制松花江流域2001年、2005年、2010年、2015年、2020年水蚀模数与风蚀模数空间分布图(图 2)。按土壤侵蚀分类分级标准将水蚀模数、风蚀模数划分为6个等级，并计算松花江流域各级土壤侵蚀的面积(表 1)。由表 1可知，2001年、2005年、2010年、2015年、2020年松花江流域均以微度水蚀或微度风蚀为主；除2020年外，流域内其余年份轻度及以上风蚀的面积均大于轻度及以上水蚀面积；2020年轻度水蚀面积远超其余年份，但中度及以上水蚀面积仍较低。
图 2 松花江流域侵蚀模数空间分布Fig. 2 Spatial distribution of soil erosion modulus in the Songhua River Basin下载:
全尺寸图片
表 1 松花江流域各级土壤侵蚀面积Table 1 Area of soil erosion at all levels of the Songhua River Basinkm2 侵蚀类型 土壤侵蚀模数等级 2001年 2005年 2010年 2015年 2020年 水蚀 微度[ < 200 t/(km2·a)] 509 874.45 488 995.98 474 034.36 492 540.59 424 059.86 轻度[200~2 500 t/(km2·a)] 39 979.32 60 815.49 75 563.49 57 294.47 125 541.15 中度[2 500~5 000 t/(km2·a)] 12.59 45.00 239.67 26.00 250.31 强度[5 000~8 000 t/(km2·a)] 1.42 8.06 19.70 5.78 12.91 极强度[8 000~15 000 t/(km2·a)] 0.07 3.03 10.00 1.06 2.99 剧烈[>15 000 t/(km2·a)] - 0.08 0.73 - 0.03 风蚀 微度[ < 200 t/(km2·a)] 491 782.07 489 353.83 487 712.29 459 513.48 481 478.96 轻度[200~2 500 t/(km2·a)] 49 959.12 49 163.24 51 434.55 69 812.66 55 488.62 中度[2 500~5 000 t/(km2·a)] 7 562.69 8 616.03 8 551.34 11 401.39 9 212.57 强度[5 000~8 000 t/(km2·a)] 2 853.72 3 939.28 3 590.23 6 078.12 4 342.78 极强度[8 000~15 000 t/(km2·a)] 1 703.08 2 479.08 2 309.59 5 155.66 2 750.63 剧烈[＞15 000 t/(km2·a)] 674.11 983.22 936.66 2 573.36 1 261.17 1.3 EM影响因子重要性验证方法
采用BORUTA算法[14]验证初步确定的16个与2种类型EM有关的影响因子的重要性。该算法适用于离散或连续型的数据，能有效识别多维影响因子中哪些影响因子对预测目标是重要的[9]。该算法主要步骤为：(1)为每个EM影响因子随机生成1个对应的阴影特征；(2)利用随机森林(RF)算法计算每个影响因子与阴影特征对EM的重要性记为Z-score，将阴影特征中的最大Z-score记为最大Z得分(MZSA)；(3)当某影响因子的Z-score大于MZSA则将其标记EM的重要影响因子，反之标记为不重要；(4)重复上述操作直至所有影响因子均被标记或达到预设的迭代次数。
1.4 基于DL的EM计算模型构建方法
本研究基于DL算法构建松花江流域的土壤侵蚀模数计算模型(简称EM模型)。
1.4.1 数据集制作
为提高侵蚀评价模型的泛化能力，随机抽取1 000个样点。以任一样点为中心在研究区域2001—2020年的数据中，逐年抽取总容量为(1 000×20)20 000的16 m×16 m大小的像元(像元面积为25 600 m2)作为样本。其中，将2001年、2005年、2010年、2015年及2020年对应(1 000×5)5 000个样本作为验证数据，其余年份均作为训练数据。分别计算每个像元的EMwa和EMwi。
1.4.2 DL模型构造与超参数设置
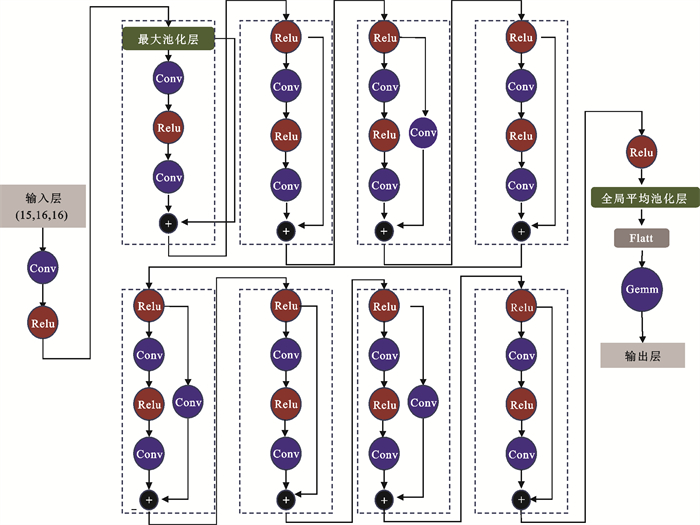
相比其他DL模型，卷积神经网络(CNN)在多维数据处理上具有更明显的优势[25]。因土壤侵蚀影响因子较多，导致CNN的输入数据维度较高，故采用CNN模型中的ResNet18[26]来构建土壤侵蚀模数计算模型。采用Relu函数为卷积后的激活函数、MSE为损失函数、adam为模型优化器、使用全局平均池化(GlobalAveragePool)代替全连接以适应输入数据的分辨率，以上编程环境为python 3.9。
详细网络结构见图 3，其中Conv代表卷积层。
图 3 ResNet18的网络结构Fig. 3 The Network Structure of ResNet18下载:
全尺寸图片
1.5 土壤侵蚀强度概率评价方法
相比于其他土壤侵蚀影响因子，降雨量、风速、气温具有较强的随机性[27-29]。因此，本研究将这3个影响因子作为随机变量，依据其概率分布，以数值模拟方法制作模拟样本，并结合高斯核密度估计法(gaussian kernel density estimation, GKDE)[30]对EM模型计算结果进行概率评价。
(1) 根据本研究使用的2001—2020年36个气象站点的3个随机变量实测数据，采用K-S检验[30]法拟合其理论分布。各气象站3个随机变量理论分布拟合结果见表 2。
表 2 松花江流域36个气象站点随机变量分布类型Table 2 The distribution types of the random variables at 36 meteorological stations in the Songhua River basin站点名 年降雨量 年平均风速 年平均日最高气温 分布类型 p值 分布类型 p值 分布类型 p值 安达 对数正态 0.97 F分布 0.91 F分布 0.56 白城 对数正态 0.95 F分布 0.93 正态分布 0.85 北安 瑞利分布 0.84 瑞利分布 0.34 F分布 0.98 东岗 瑞利分布 0.99 F分布 0.68 正态分布 0.87 敦化 对数正态 0.99 F分布 0.70 正态分布 0.50 扶余 F分布 0.91 对数正态 0.86 F分布 0.63 富锦 F分布 0.95 F分布 0.98 F分布 0.94 富裕 F分布 0.94 F分布 0.93 正态分布 0.73 哈尔滨 对数正态 0.98 F分布 0.93 F分布 0.99 海伦 对数正态 0.99 F分布 0.88 正态分布 0.90 桦甸 卡方分布 0.99 F分布 0.95 F分布 0.54 佳木斯 F分布 0.99 对数正态 0.17 F分布 0.99 蛟河 伽马分布 0.99 F分布 0.74 正态分布 0.75 靖宇 F分布 0.93 对数正态 0.96 正态分布 0.76 克山 F分布 0.89 F分布 0.75 正态分布 0.90 梅河口 F分布 0.95 对数正态 0.95 正态分布 0.33 明水 F分布 0.92 F分布 0.46 F分布 0.93 嫩江 F分布 0.86 F分布 0.98 正态分布 0.95 盘石 瑞利分布 0.58 F分布 0.77 正态分布 0.53 齐齐哈尔 瑞利分布 0.98 对数正态 0.88 均匀分布 0.79 前郭尔罗斯 瑞利分布 0.90 F分布 0.80 均匀分布 0.78 乾安 瑞利分布 0.99 F分布 0.73 F分布 0.40 尚志 F分布 0.97 F分布 0.75 F分布 0.97 松江 瑞利分布 0.96 F分布 0.78 正态分布 0.73 索伦 F分布 0.96 对数正态 0.80 正态分布 0.66 泰来 F分布 0.94 瑞利分布 0.10 正态分布 0.80 铁力 F分布 0.93 指数分布 0.67 正态分布 0.95 通河 对数正态 0.89 对数正态 0.95 瑞利分布 0.89 通榆 对数正态 0.93 F分布 0.60 正态分布 0.60 小二沟 对数正态 0.86 F分布 0.73 正态分布 0.94 伊春 F分布 0.93 对数正态 0.98 F分布 0.90 依兰 瑞利分布 0.36 对数正态 0.95 F分布 0.99 永吉 伽马分布 0.86 F分布 0.81 F分布 0.59 扎兰屯 对数正态 0.51 对数正态 0.52 F分布 0.59 长岭 伽马分布 0.80 F分布 0.34 F分布 0.47 肇州 F分布 0.78 F分布 0.92 均匀分布 0.80 注：显著性水平p=0.05。 (2) 对于每个气象站，依据其3个随机变量的理论分布，采用数值模拟方法生成各变量的伪随机数1 000个作为随机样本；以该站所在像元作为典型像元，将其3个随机变量的样本(1 000个)分别与2020年其他土壤侵蚀影响因子(忽略其他影响因子的随机性)组合成1 000个模拟样本向量，作为土壤侵蚀模数计算模型的输入。
(3) 将全部模拟样本输入到训练好的EM计算模型中得到相应的EMwa与EMwi；并采用高斯核密度估计法[30]绘制EMwa与EMwi的联合分布；再通过积分计算不同EMwa与EMwi强度等级组合的发生概率。
2. 结果与分析
2.1 EM影响因子重要性验证结果
为降低模型输入数据的噪声及冗余、提高EM模型的鲁棒性和计算效率，采用BORUTA算法[14]分析16个EM影响因子的重要性，进而剔除EM的弱相关变量。
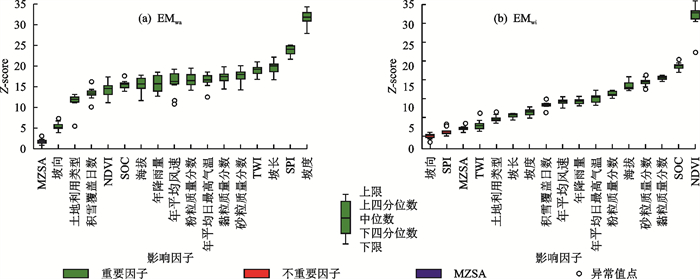
将BORUTA算法[14]每次迭代计算的各因子(包括MZSA)Z-score绘制成箱线图(图 4)，并用不同颜色分类表示重要因子(绿)、不重要因子(红)及MZSA(蓝)。由图 4可以看出，所有影响因子均为EMwa的重要因子；除坡向与SPI外，所有影响因子均为EMwi的重要因子。由于同一影响因子对2种侵蚀类型的重要性得分差异较大，为便于比并有效地筛选对2种侵蚀都有重要影响的因子，从而剔除对2种侵蚀均影响较小的因子，现定义相对重要性(relative importance，RI)指标，其计算方法为：
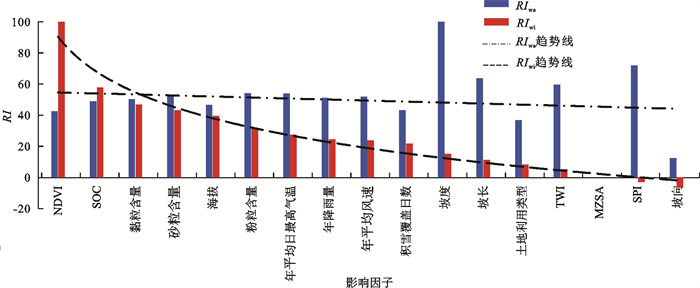
$$ R I_i=\left(Z_i-\mathrm{MZSA}_i\right) /\left(Z_{\max -i}-\mathrm{MZSA}_i\right) $$ (4) 
图 4 土壤侵蚀模数影响因子重要性分析结果Fig. 4 Analysis results of the importance of soil erosion modulus impact factors下载:
全尺寸图片
式中：RIi为某因子对EMwa或EMwi的相对重要性(百分数计)，分别记为RIwa、RIwi；Zi为对应侵蚀类型EM下该因子的Z-score，分别记为Zwa、Zwi；MZSAi为对应侵蚀类型EM的MZSA，分别记为MZSAwa、MZSAwi；Zmax-i为对应侵蚀类型EM影响因子的Z-score最大值，分别记为Zmax-wa、Zmax-wi；Zi、MZSAi、Zmax-i均取BORUTA算法多次迭代后的中位数。RIwa、RIwi计算结果见图 5。由图 5可以看出，RIwi的最大值与最小值分别为NDVI(100%)和坡向(-6.72%)；RIwa的最大值与最小值分别为除坡度(100%)和坡向(12.32%)。
图 5 各影响因子的RIwa、RIwiFig. 5 The RIwa and RIwi of each impact factor下载:
全尺寸图片
综合对图 4、图 5的分析结果可知，RIwa与RIwi的最小值均为坡向，且该因子为EMwi的不重要因子，因此坡向不作为EM模型的输入变量；SPI作为EMwi的另一个不重要因子，由于其对于EMwi的相对重要性较高(71.86%)，因此保留该因子作为EM模型的输入变量。综上，剔除EM模型唯一的弱相关变量(坡向)，使其输入变量为除坡向外的15个影响因子。
2.2 EM模型的构建及应用
2.2.1 模型的构建及验证
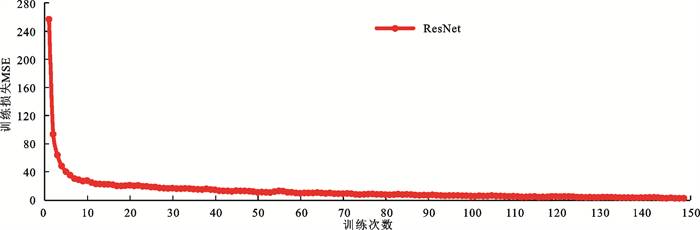
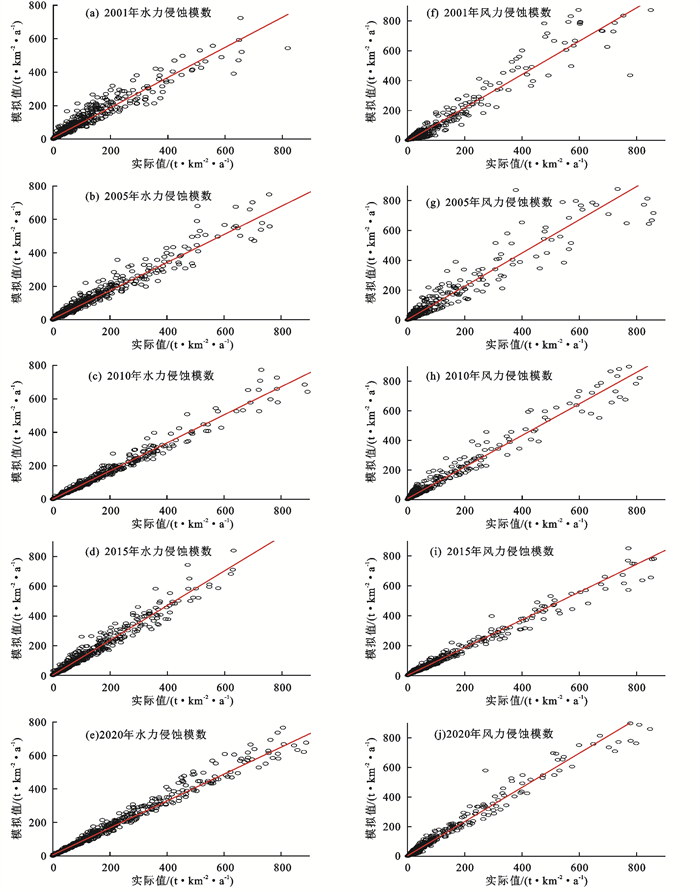
EM模型输入为已确定的15个重要影响因子对应训练样本，输出为水蚀模数和风蚀模数，模型训练次数设定为150次，模拟收敛条件设定为MSE＜5，每次训练所对应的损失值迭代曲线见图 6。图 6显示模型损失下降梯度较快，在第120次训练后(4.81)，EM模型达到收敛条件，模型构建成功。为进一步验证收敛后土壤侵蚀模型的有效性，现计算验证数据中每年对应侵蚀模数的决定系数(R2)并绘制EMwa、EMwi的实际值与模拟值散点图(表 3、图 7)可以看出，验证期的R2均>0.86。综合以上分析表明，所构建的EM模型具有较高计算精度，可用于松花江流域土壤侵蚀模数的预测。
图 6 EM模型每次训练对应损失值Fig. 6 A loss value curve for each training of the EM model下载:
全尺寸图片
表 3 验证期EM模型R2Table 3 Validation period EM calculation model R2EM类型 2001年 2005年 2010年 2015年 2020年 EMwa 0.88 0.87 0.91 0.92 0.91 EMwi 0.86 0.88 0.91 0.93 0.90 
图 7 EM模拟值与实际值散点图Fig. 7 Scatter plot of simulated and actual soil erosion values下载:
全尺寸图片
2.2.2 松花江流域EM计算结果
基于松花江流域所有像元的土壤侵蚀影响因子数据，利用已构建的EM模型计算整个流域的EMwa、EMwi(空间分辨率为1 600 m×1 600 m)，根据土壤侵蚀分类分级标准结合松花江流域土壤侵蚀实际情况，分别将EMwa与EMwi划分为微度、轻度、中度、重度4个强度等级，将某一水蚀强度等级与某一风蚀强度等级组合命名为侵蚀强度组合，不同侵蚀强度组合见表 4。
表 4 侵蚀强度组合Table 4 Erosion intensity level combination水蚀强度 风蚀强度 微度
[ < 200 t/(km2·a)]轻度
[200~2 500 t/(km2·a)]中度
[2 500~5 000 t/(km2·a)]重度
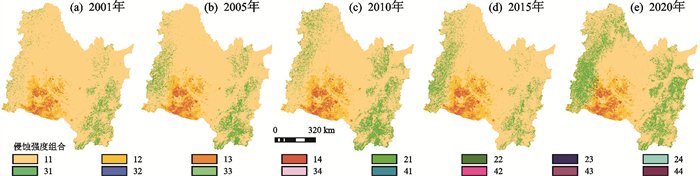
[>5 000 t/(km2·a)]微度[＜200 t/(km2·a)] 11 12 13 14 轻度[200~2 500 t/(km2·a)] 21 22 23 24 中度[2 500~5 000 t/(km2·a)] 31 32 33 34 重度[＞5 000 t/(km2·a)] 41 42 43 44 注：十位数字代表水蚀强度，个位数字代表风蚀强度。 基于EM模型计算得出的松花江流域EMwa、EMwi，绘制验证期(2001年、2005年、2010年、2015年、2020年流域内侵蚀强度组合空间分布图(图 8)，并统计验证期每年各等级EM占流域总面积的比例(表 5)。由图 8可知，松花江流域土壤侵蚀强度组合空间分布特征体现为东西两侧山脉水蚀强度高于风蚀强度、中部平原风力侵蚀强度高于水蚀强度，与图 1所反映的东西两侧山脉EMwa＞EMwi、中部风蚀模数EMwi＞EMwa的规律一致。说明所构建的系统模型在松花江流域具有较好的适用性。由表 5可知，流域内平均每年发生微度水蚀与微度风蚀的面积占比为74.47%，该强度组合面积随时间推移呈下降趋势，说明流域内土壤侵蚀强度有逐渐加重的趋势。流域内平均每年发生轻度水蚀与微度风蚀的面积占比为12.69%，微度水蚀与轻度风蚀的面积占比为9.47%，微度水蚀与中度风蚀的面积占比为1.75%，微度水蚀与重度风蚀的面积占比为1.33%，轻度水蚀与轻度风蚀的面积占比为0.17%，轻度水蚀轻度风蚀的面积占比为0.10%，其余水蚀与风蚀强度组合面积占比极小(< 0.01%)。
图 8 验证期侵蚀强度组合空间分布Fig. 8 Spatial distribution of erosion intensity combinations during the validation period下载:
全尺寸图片
表 5 验证期各土壤侵蚀强度组合面积占比Table 5 Area share of each soil erosion intensity combination during the validation period% 侵蚀强度组合 2001年 2005年 2010年 2015年 2020年 年平均值 11 81.49 77.31 72.55 75.93 65.08 74.47 12 8.92 8.69 10.33 10.28 9.14 9.47 13 1.44 1.69 1.94 1.94 1.74 1.75 14 0.94 1.33 1.51 1.51 1.36 1.33 21 7.18 10.86 13.33 10.25 21.81 12.69 22 0.01 0.03 0.01 0.06 0.40 0.10 23 0 0 0 0 0.03 0.01 24 0 0 0 0 0.01 0 31 0.01 0.08 0.32 0.02 0.42 0.17 32 0 0 0 0 0 0 33 0 0 0 0 0 0 34 0 0 0 0 0 0 41 0 0 0.01 0 0 0 42 0 0 0 0 0 0 43 - - 0 0 0 0 44 - - 0 - 0 0 总计 100.00 100.00 100.00 100.00 100.00 100.00 2.3 松花江流域土壤侵蚀概率评价
采用高斯核函数估计方法计算系统模型输出的36个典型像元(以对应的气象站名称命名)EMwa与EMwi联合密度，并绘制联合密度曲面图(图 9)。对联合分布函数求积分，即可得到不同侵蚀强度组合发生的概率，对36个像元各侵蚀强度组合发生概率求平均值(表 6)。由表 6可知，36个典型像元中，发生微度水蚀与微度风蚀的平均概率为57.45%；发生微度水蚀与轻度风蚀的平均概率为30.26%；发生微度水蚀与中度风蚀的平均概率为8.03%；发生轻度水蚀与微度风蚀的平均概率为2.11%；发生微度水蚀与重度风蚀的平均概率为2.08%；发生轻度水蚀与轻度风蚀的平均概率为0.04%；发生其余侵蚀强度组合的平均概率均≤0.01%。
图 9 松花江流域内36个典型像元EMwa与EMwi联合分布Fig. 9 Joint distribution of EMwa and EMwi for the 36 typical pixels in the Songhua River Basin下载:
全尺寸图片
表 6 36个典型像元各侵蚀强度组合的平均发生概率Table 6 Average probability of occurrence for each combination of erosion intensities for 36 typical image elements% 水蚀强度 风蚀强度 微度 轻度 中度 重度 微度 57.45 30.26 8.03 2.08 轻度 2.11 0.04 - - 中度 0.01 - - - 重度 0.01 0.01 - - 3. 讨论
本研究中EM的预测结果表明，研究区内大部分区域EM较低，两侧山脉EMwa较高、中部平原EMwi较高，与已有研究[2, 5-6]发现的松花江流域土壤侵蚀以微度为主、水力侵蚀集中在长白山脉及大兴安岭地区、风力侵蚀集中在中南部平原的成果相符，即松花江流域内山区更易发生水力侵蚀、平原则容易发生风力侵蚀。本研究中2020年EMwa明显高于其他年份，其原因可能是2020年流域内降雨量较高，导致降雨侵蚀力增加进而使得流域内EMwa升高，与吴瀚逸等[6]提出的2001—2020年中国东北区域土壤水蚀数据集中所表现的2020年松花江流域内轻度以上水蚀面积明显大于其他年份的结果是一致的。
本研究发现，松花江流域水力侵蚀与风力侵蚀空间上呈近似负相关[5]，与左小峰等[4]黑土风洞试验发现风蚀对坡面水蚀有一定促进作用的结论不同。究其原因可能是本研究的流域空间、年际时间的尺度较大，难以有效表现年内小尺度条件下土壤侵蚀的变化规律，因此，有必要在未来对不同时空尺度的土壤侵蚀变化差异开展进一步的研究。REZAEI等[12]对基于深度学习的风蚀模型结果的不确定性进行量化分析[12]。由于其输入变量的随机性研究不够深入，故本研究基于降雨、气温、风速3个随机变量的概率密度进行数值模拟，考虑土壤侵蚀影响因子的随机性；同时使用高斯核密度法给出基于数值模拟结果计算出的不同强度等级EM组合的发生概率，更直观反映出土壤侵蚀的随机性。
各典型像元中，发生轻度及以上风蚀与微度水蚀组合的概率较高，其原因主要是流域中部风力侵蚀较重的区域典型像元较多，导致各典型像元发生轻度风蚀与微度水蚀、中度风蚀与微度水蚀、重度风蚀与微度水蚀3个侵蚀强度组合的平均发生概率偏高，同时说明松花江流域中部区域风力侵蚀强度较大，应采取相应的治理措施。
本文采用吴瀚逸等[6]制作的土壤水蚀数据集及RWEQ计算得到的风蚀模数数据作为训练数据，构建松花江流域的土壤侵蚀模数(EM)计算模型，并且模型具有较高的精度。对于松花江流域以外的东北地区，由于地形、气象、土壤及土地覆盖等因素未发生显著变化，模型精度仍有保障。然而，对于黄土高原、青藏高原等自然条件与东北地区存在显著差异的地区，该模型需重新训练后方可适用。
4. 结论
(1) 利用Boruta算法对可能影响松花江流域土壤侵蚀模数(EM)的16个因子进行的验证。结果显示，除坡向因子外，其余15个影响因子均为松花江流域EM的重要影响因子。
(2) 通过构建基于DL的EM的计算模型，评价松花江流域内土壤侵蚀强度组合空间分布。结果显示，流域内平均每年有74.47%发生微度水蚀与微度风蚀, 12.86%的面积发生轻度及以上水蚀与微度风蚀, 12.56%的面积发生轻度及以上风蚀与微度水蚀, 0.11%的面积水蚀强度与风蚀强度均在轻度及以上。
(3) 采用非参数拟合技术及高斯核密度估计(GKDE)，对松花江流域内36个典型像元土壤侵蚀强度进行概率评价。结果显示，36个典型像元中，发生微度水蚀与微度风蚀的平均概率为57.45%, 发生微度水蚀与轻度风蚀的平均概率为30.26%, 发生微度水蚀与中度风蚀的平均概率为8.03%, 发生轻度水蚀与微度风蚀的平均概率为2.11%, 发生微度水蚀与重度风蚀的平均概率为2.08%, 发生轻度水蚀与轻度风蚀的平均概率为0.04%, 发生其余侵蚀强度组合的平均概率均≤0.01%。
(4) 构建的基于DL和GKDE的土壤侵蚀概率评价模型能够有效地揭示松花江流域侵蚀的空间分布特征，同时给出2种侵蚀类型不同强度组合的发生概率。研究成果拓展了土壤侵蚀评价结果的表现形式，同时可为松花江流域土壤侵蚀治理提供决策依据。
-
图 1 松花江流域位置
Fig. 1 Map of the Songhua River basin location
下载:
全尺寸图片
图 2 松花江流域侵蚀模数空间分布
Fig. 2 Spatial distribution of soil erosion modulus in the Songhua River Basin
下载:
全尺寸图片
图 3 ResNet18的网络结构
Fig. 3 The Network Structure of ResNet18
下载:
全尺寸图片
图 4 土壤侵蚀模数影响因子重要性分析结果
Fig. 4 Analysis results of the importance of soil erosion modulus impact factors
下载:
全尺寸图片
图 5 各影响因子的RIwa、RIwi
Fig. 5 The RIwa and RIwi of each impact factor
下载:
全尺寸图片
图 6 EM模型每次训练对应损失值
Fig. 6 A loss value curve for each training of the EM model
下载:
全尺寸图片
图 7 EM模拟值与实际值散点图
Fig. 7 Scatter plot of simulated and actual soil erosion values
下载:
全尺寸图片
图 8 验证期侵蚀强度组合空间分布
Fig. 8 Spatial distribution of erosion intensity combinations during the validation period
下载:
全尺寸图片
图 9 松花江流域内36个典型像元EMwa与EMwi联合分布
Fig. 9 Joint distribution of EMwa and EMwi for the 36 typical pixels in the Songhua River Basin
下载:
全尺寸图片
表 1 松花江流域各级土壤侵蚀面积
Table 1 Area of soil erosion at all levels of the Songhua River Basin
km2 侵蚀类型 土壤侵蚀模数等级 2001年 2005年 2010年 2015年 2020年 水蚀 微度[ < 200 t/(km2·a)] 509 874.45 488 995.98 474 034.36 492 540.59 424 059.86 轻度[200~2 500 t/(km2·a)] 39 979.32 60 815.49 75 563.49 57 294.47 125 541.15 中度[2 500~5 000 t/(km2·a)] 12.59 45.00 239.67 26.00 250.31 强度[5 000~8 000 t/(km2·a)] 1.42 8.06 19.70 5.78 12.91 极强度[8 000~15 000 t/(km2·a)] 0.07 3.03 10.00 1.06 2.99 剧烈[>15 000 t/(km2·a)] - 0.08 0.73 - 0.03 风蚀 微度[ < 200 t/(km2·a)] 491 782.07 489 353.83 487 712.29 459 513.48 481 478.96 轻度[200~2 500 t/(km2·a)] 49 959.12 49 163.24 51 434.55 69 812.66 55 488.62 中度[2 500~5 000 t/(km2·a)] 7 562.69 8 616.03 8 551.34 11 401.39 9 212.57 强度[5 000~8 000 t/(km2·a)] 2 853.72 3 939.28 3 590.23 6 078.12 4 342.78 极强度[8 000~15 000 t/(km2·a)] 1 703.08 2 479.08 2 309.59 5 155.66 2 750.63 剧烈[＞15 000 t/(km2·a)] 674.11 983.22 936.66 2 573.36 1 261.17 表 2 松花江流域36个气象站点随机变量分布类型
Table 2 The distribution types of the random variables at 36 meteorological stations in the Songhua River basin
站点名 年降雨量 年平均风速 年平均日最高气温 分布类型 p值 分布类型 p值 分布类型 p值 安达 对数正态 0.97 F分布 0.91 F分布 0.56 白城 对数正态 0.95 F分布 0.93 正态分布 0.85 北安 瑞利分布 0.84 瑞利分布 0.34 F分布 0.98 东岗 瑞利分布 0.99 F分布 0.68 正态分布 0.87 敦化 对数正态 0.99 F分布 0.70 正态分布 0.50 扶余 F分布 0.91 对数正态 0.86 F分布 0.63 富锦 F分布 0.95 F分布 0.98 F分布 0.94 富裕 F分布 0.94 F分布 0.93 正态分布 0.73 哈尔滨 对数正态 0.98 F分布 0.93 F分布 0.99 海伦 对数正态 0.99 F分布 0.88 正态分布 0.90 桦甸 卡方分布 0.99 F分布 0.95 F分布 0.54 佳木斯 F分布 0.99 对数正态 0.17 F分布 0.99 蛟河 伽马分布 0.99 F分布 0.74 正态分布 0.75 靖宇 F分布 0.93 对数正态 0.96 正态分布 0.76 克山 F分布 0.89 F分布 0.75 正态分布 0.90 梅河口 F分布 0.95 对数正态 0.95 正态分布 0.33 明水 F分布 0.92 F分布 0.46 F分布 0.93 嫩江 F分布 0.86 F分布 0.98 正态分布 0.95 盘石 瑞利分布 0.58 F分布 0.77 正态分布 0.53 齐齐哈尔 瑞利分布 0.98 对数正态 0.88 均匀分布 0.79 前郭尔罗斯 瑞利分布 0.90 F分布 0.80 均匀分布 0.78 乾安 瑞利分布 0.99 F分布 0.73 F分布 0.40 尚志 F分布 0.97 F分布 0.75 F分布 0.97 松江 瑞利分布 0.96 F分布 0.78 正态分布 0.73 索伦 F分布 0.96 对数正态 0.80 正态分布 0.66 泰来 F分布 0.94 瑞利分布 0.10 正态分布 0.80 铁力 F分布 0.93 指数分布 0.67 正态分布 0.95 通河 对数正态 0.89 对数正态 0.95 瑞利分布 0.89 通榆 对数正态 0.93 F分布 0.60 正态分布 0.60 小二沟 对数正态 0.86 F分布 0.73 正态分布 0.94 伊春 F分布 0.93 对数正态 0.98 F分布 0.90 依兰 瑞利分布 0.36 对数正态 0.95 F分布 0.99 永吉 伽马分布 0.86 F分布 0.81 F分布 0.59 扎兰屯 对数正态 0.51 对数正态 0.52 F分布 0.59 长岭 伽马分布 0.80 F分布 0.34 F分布 0.47 肇州 F分布 0.78 F分布 0.92 均匀分布 0.80 注：显著性水平p=0.05。 表 3 验证期EM模型R2
Table 3 Validation period EM calculation model R2
EM类型 2001年 2005年 2010年 2015年 2020年 EMwa 0.88 0.87 0.91 0.92 0.91 EMwi 0.86 0.88 0.91 0.93 0.90 表 4 侵蚀强度组合
Table 4 Erosion intensity level combination
水蚀强度 风蚀强度 微度
[ < 200 t/(km2·a)]轻度
[200~2 500 t/(km2·a)]中度
[2 500~5 000 t/(km2·a)]重度
[>5 000 t/(km2·a)]微度[＜200 t/(km2·a)] 11 12 13 14 轻度[200~2 500 t/(km2·a)] 21 22 23 24 中度[2 500~5 000 t/(km2·a)] 31 32 33 34 重度[＞5 000 t/(km2·a)] 41 42 43 44 注：十位数字代表水蚀强度，个位数字代表风蚀强度。 表 5 验证期各土壤侵蚀强度组合面积占比
Table 5 Area share of each soil erosion intensity combination during the validation period
% 侵蚀强度组合 2001年 2005年 2010年 2015年 2020年 年平均值 11 81.49 77.31 72.55 75.93 65.08 74.47 12 8.92 8.69 10.33 10.28 9.14 9.47 13 1.44 1.69 1.94 1.94 1.74 1.75 14 0.94 1.33 1.51 1.51 1.36 1.33 21 7.18 10.86 13.33 10.25 21.81 12.69 22 0.01 0.03 0.01 0.06 0.40 0.10 23 0 0 0 0 0.03 0.01 24 0 0 0 0 0.01 0 31 0.01 0.08 0.32 0.02 0.42 0.17 32 0 0 0 0 0 0 33 0 0 0 0 0 0 34 0 0 0 0 0 0 41 0 0 0.01 0 0 0 42 0 0 0 0 0 0 43 - - 0 0 0 0 44 - - 0 - 0 0 总计 100.00 100.00 100.00 100.00 100.00 100.00 表 6 36个典型像元各侵蚀强度组合的平均发生概率
Table 6 Average probability of occurrence for each combination of erosion intensities for 36 typical image elements
% 水蚀强度 风蚀强度 微度 轻度 中度 重度 微度 57.45 30.26 8.03 2.08 轻度 2.11 0.04 - - 中度 0.01 - - - 重度 0.01 0.01 - - -
[1] ZHU Y L, LI W B, WANG D Y, et al. Spatial pattern of soil erosion in relation to land use change in a rolling hilly region of Northeast China[J]. Land, 2022, 11(8): e1253. doi: 10.3390/land11081253 [2] WANG X, ZHAO X L, ZHANG Z X, et al. Assessment of soil erosion change and its relationships with land use/cover change in China from the end of the 1980s to 2010[J]. Catena, 2016, 137: 256-268. doi: 10.1016/j.catena.2015.10.004 [3] WANG H, YANG S L, WANG Y D, et al. Rates and causes of black soil erosion in Northeast China[J]. Catena, 2022, 214: e106250. doi: 10.1016/j.catena.2022.106250 [4] 左小锋, 郑粉莉, 张加琼, 等. 典型薄层黑土区前期地表风蚀作用影响坡面水蚀的研究[J]. 土壤学报, 2021, 58(5): 1145-1156. ZUO X F, ZHENG F L, ZHANG J Q, et al. Study on effect of surface wind erosion on hillslope water erosion in regions of typical thin layered mollisol at early stages[J]. Acta Pedologica Sinica, 2021, 58(5): 1145-1156. [5] WANG S H, XU X L, HUANG L. Spatial and temporal variability of soil erosion in Northeast China from 2000 to 2020[J]. Remote Sensing, 2022, 15(1): e225. doi: 10.3390/rs15010225 [6] 吴瀚逸, 熊俊峰, 侯渲, 等. 2001—2020年中国东北区域土壤水蚀数据集[J]. 中国科学数据, 2023, 8(4): 283-297. WU H Y, XIONG J F, HOU X, et al. A dataset of soil water erosion of Northeast China from 2001 to 2020[J]. China Scientific Data, 2023, 8(4): 283-297. [7] 杨严攀, 田培, 沈晨竹, 等. 基于RUSLE模型和地理探测器的鄂西南土壤侵蚀脆弱性评价[J]. 水土保持学报, 2024, 38(1): 91-103. http://stbcxb.alljournal.com.cn/stbcxb/article/abstract/20240110?st=search YANG Y P, TIAN P, SHEN C Z, et al. Vulnerability assessment of soil erosion in southwestern Hubei Province based on RUSLE model and geographic detector[J]. Journal of Soil and Water Conservation, 2024, 38(1): 91-103. http://stbcxb.alljournal.com.cn/stbcxb/article/abstract/20240110?st=search [8] 池金洺, 于洋, 冯娟龙, 等. 基于RUSLE模型的妫水河流域土壤侵蚀时空变化特征[J]. 水土保持学报, 2024, 38(1): 70-78. http://stbcxb.alljournal.com.cn/stbcxb/article/abstract/20240108?st=search CHI J M, YU Y, FENG J L, et al. Spatialand temporal variation characteristics of soil erosion in Guishui River Basin based on RUSLE[J]. Journal of Soil and Water Conservation, 2024, 38(1): 70-78. http://stbcxb.alljournal.com.cn/stbcxb/article/abstract/20240108?st=search [9] GHOLAMI H, MOHAMMADIFAR A, GOLZARI S, et al. Using the Boruta algorithm and deep learning models for mapping land susceptibility to atmospheric dust emissions in Iran[J]. Aeolian Research, 2021, 50: e100682. doi: 10.1016/j.aeolia.2021.100682 [10] KHOSRAVI K, REZAIE F, COOPER J R, et al. Soil water erosion susceptibility assessment using deep learning algorithms[J]. Journal of Hydrology, 2023, 618: e129229. doi: 10.1016/j.jhydrol.2023.129229 [11] 郑粉莉, 张加琼, 刘刚, 等. 东北黑土区坡耕地土壤侵蚀特征与多营力复合侵蚀的研究重点[J]. 水土保持通报, 2019, 39(4): 314-319. ZHENG F L, ZHANG J Q, LIU G, et al. Characteristics of soil erosion on sloping farmlands and key fields for studying compound soil erosion caused by multi-forces in mollisol region of Northeast China[J]. Bulletin of Soil and Water Conservation, 2019, 39(4): 314-319. [12] REZAEI M, MOHAMMADIFAR A, GHOLAMI H, et al. Mapping of the wind erodible fraction of soil by bidirectional gated recurrent unit (BiGRU) and bidirectional recurrent neural network (BiRNN) deep learning models[J]. Catna, 2023, 223: e106953. doi: 10.1016/j.catena.2023.106953 [13] 王善序. 贝叶斯概率水文预报简介[J]. 水文, 2001, 21(5): 33-34. doi: 10.3969/j.issn.1000-0852.2001.05.009 WANG S X. Introduction to the Bayesian forecasting system[J]. Hydrology, 2001, 21(5): 33-34. doi: 10.3969/j.issn.1000-0852.2001.05.009 [14] CIMUSA K L, BIGABWA B J, PRASAD P, et al. Soil erosion susceptibility mapping using ensemble machine learning models: A case study of upper Congo River sub-basin[J]. Catena, 2023, 222: e106858. doi: 10.1016/j.catena.2022.106858 [15] BAG R, MONDAL I, DEHBOZORGI M, et al. Modelling and mapping of soil erosion susceptibility using machine learning in a tropical hot sub-humid environment[J]. Journal of Cleaner Production, 2022, 364: e132428. doi: 10.1016/j.jclepro.2022.132428 [16] 张光辉, 杨扬, 刘瑛娜, 等. 东北黑土区土壤侵蚀研究进展与展望[J]. 水土保持学报, 2022, 36(2): 1-12. http://stbcxb.alljournal.com.cn/stbcxb/article/abstract/20220201?st=search ZHANG G H, YANG Y, LIU Y N, et al. Advances and prospects of soil erosion research in the black soil region of Northeast China[J]. Journal of Soil and Water Conservation, 2022, 36(2): 1-12. http://stbcxb.alljournal.com.cn/stbcxb/article/abstract/20220201?st=search [17] 焦剑, 谢云, 林燕, 等. 东北地区融雪期径流及产沙特征分析[J]. 地理研究, 2009, 28(2): 333-344. doi: 10.3321/j.issn:1000-0585.2009.02.007 JIAO J, XIE Y, LIN Y, et al. Study on snowmelt runoff and sediment yields in Northeast China[J]. Geographical Research, 2009, 28(2): 333-344. doi: 10.3321/j.issn:1000-0585.2009.02.007 [18] 张晓敏, 张东梅, 王莉, 等. 降雨、积雪以及土地利用复合影响下的额尔齐斯河流域土壤侵蚀分析[J]. 水土保持学报, 2022, 36(5): 104-111. http://stbcxb.alljournal.com.cn/stbcxb/article/abstract/20220515?st=search ZHANG X M, ZHANG D M, WANG L, et al. Soil erosion analysis in the Irtysh River Basin under the combined effects of rainfall, snow cover and land use[J]. Journal of Soil and Water Conservation, 2022, 36(5): 104-111. http://stbcxb.alljournal.com.cn/stbcxb/article/abstract/20220515?st=search [19] 赵琴, 郝晓华, 王建, 等. 2000—2020年MODIS中国积雪物候数据集[D/OL]. 国家冰川冻土沙漠科学数据中心(www. ncdc. ac. cn), 2021. https://cstr.cn/CSTR:11738.11.ncdc.isnow.db2519.2022. ZHAO Q, HAO X H, WANG J, et al. A dataset of snow cover phenology in China based on MODIS during 2000—2020[D/OL]. National Cryosphere Desert Data Center (www. ncdc. ac. cn), 2021. https://cstr.cn/CSTR:11738.11.ncdc.isnow.db2519.2022. [20] 赵琴, 郝晓华, 王建, 等. 2000—2020年MODIS中国积雪物候数据集[J]. 中国科学数据, 2022, 7(3): 60-69. ZHAO Q, HAO X H, WANG J, et al. A dataset of snow cover phenology in China based on MODIS during 2000—2020[J]. China Scientific Data, 2022, 7(3): 60-69. [21] YANG J, HUANG X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019[J]. Earth System Science Data, 2021, 13(8): 3907-3925. doi: 10.5194/essd-13-3907-2021 [22] 刘峰, 张甘霖. 中国高分辨率国家土壤信息网格基本属性数据集(2010—2018)[ED/OL]. 国家青藏高原数据中心, 2021. https://doi.org/10.11666/00073.ver1.db. LIU F, ZHANG G L. Basic soil property dataset of high-resolution China Soil Information Grids (2010—2018)[ED/OL]. National Tibetan Plateau Data Center, 2021. https://dx.doi.org/10.11666/00073.ver1.db. [23] LIU F, ZHANG G L, SONG X D, et al. High-resolution and three-dimensional mapping of soil texture of China[J]. Geoderma, 2020, 361: e114061. doi: 10.1016/j.geoderma.2019.114061 [24] 巩国丽, 刘纪远, 邵全琴. 基于RWEQ的20世纪90年代以来内蒙古锡林郭勒盟土壤风蚀研究[J]. 地理科学进展, 2014, 33(6): 825-834. GONG G L, LIU J Y, SHAO Q Q. Wind erosion in Xilingol League, Inner Mongolia since the 1990s using the Revised Wind Erosion Equation[J]. Progress in Geography, 2014, 33(6): 825-834. [25] 张天骐, 柏浩钧, 叶绍鹏, 等. 基于注意力门控膨胀卷积网络的单通道语音增强[J]. 电子与信息学报, 2022, 44(9): 3277-3288. ZHANG T Q, BAI H J, YE S P, et al. Monaural speech enhancement based on attention-gate dilated convolution network[J]. Journal of Electronics and Information Technology, 2022, 44(9): 3277-3288. [26] HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition//2016. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA. IEEE, 2016: 770-778. [27] 王红瑞, 林欣, 刘琼, 等. 基于系统聚类的北京气温变化过程遍历特征分析[J]. 系统工程理论与实践, 2010, 30(2): 193-200. WANG H R, LIN X, LIU Q, et al. Ergodicity analysis based on system clustering for temperature variation process of Beijing[J]. Systems Engineering-Theory and Practice, 2010, 30(2): 193-200. [28] 贺敬, 李少林, 蔡玮, 等. 双重不确定性预测下风电场超短期有功优化控制[J]. 太阳能学报, 2023, 44(11): 270-278. HE J, LI S L, CAI W, et al. Optimal control of wind farm power based on double uncertainty prediction[J]. Acta Energiae Solaris Sinica, 2023, 44(11): 270-278. [29] 庄琦, 刘曙光, 周正正. 降雨数据时空精度对城市暴雨变异性及频率分析的影响[J]. 水科学进展, 2023, 34(3): 398-408. ZHUANG Q, LIU S G, ZHOU Z Z. Impact of rainfall spatiotemporal resolutions on urban extreme rainfall variability and rainfall frequency analysis[J]. Advances in Water Science, 2023, 34(3): 398-408. [30] 程媛, 迟荣华, 黄少滨, 等. 基于非参数密度估计的不确定轨迹预测方法[J]. 自动化学报, 2019, 45(4): 787-798. CHENG Y, CHI R H, HUANG S B, et al. Uncertain trajectory prediction method using non-parametric density estimation[J]. Acta Automatica Sinica, 2019, 45(4): 787-798.
